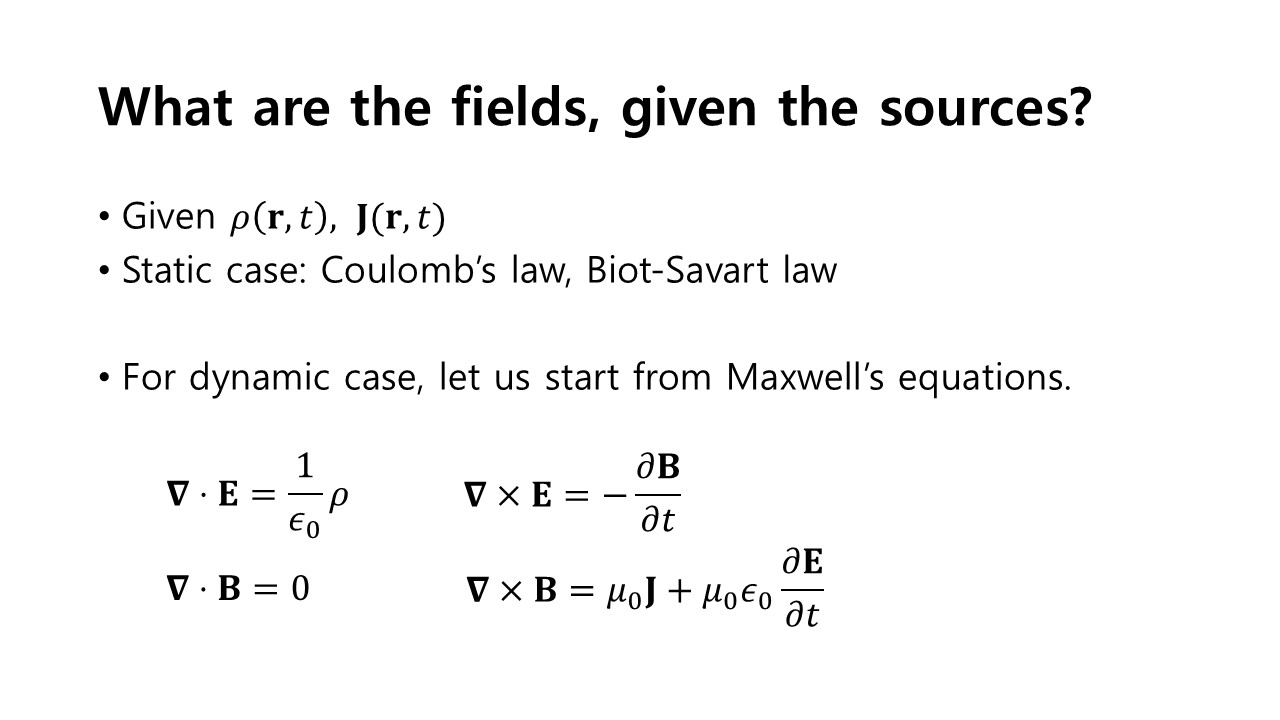10. Potentials and Fields

In this article, we study the general solution to Maxwell's equations.

The Potential Formulation

We have studied in previous chapters the potentials and fields in static case, given the charge and current sources. What would the potentials and fields look like in dynamic case? Griffith invites us to the general form of potentials and fields, starting from Maxwell's equations.

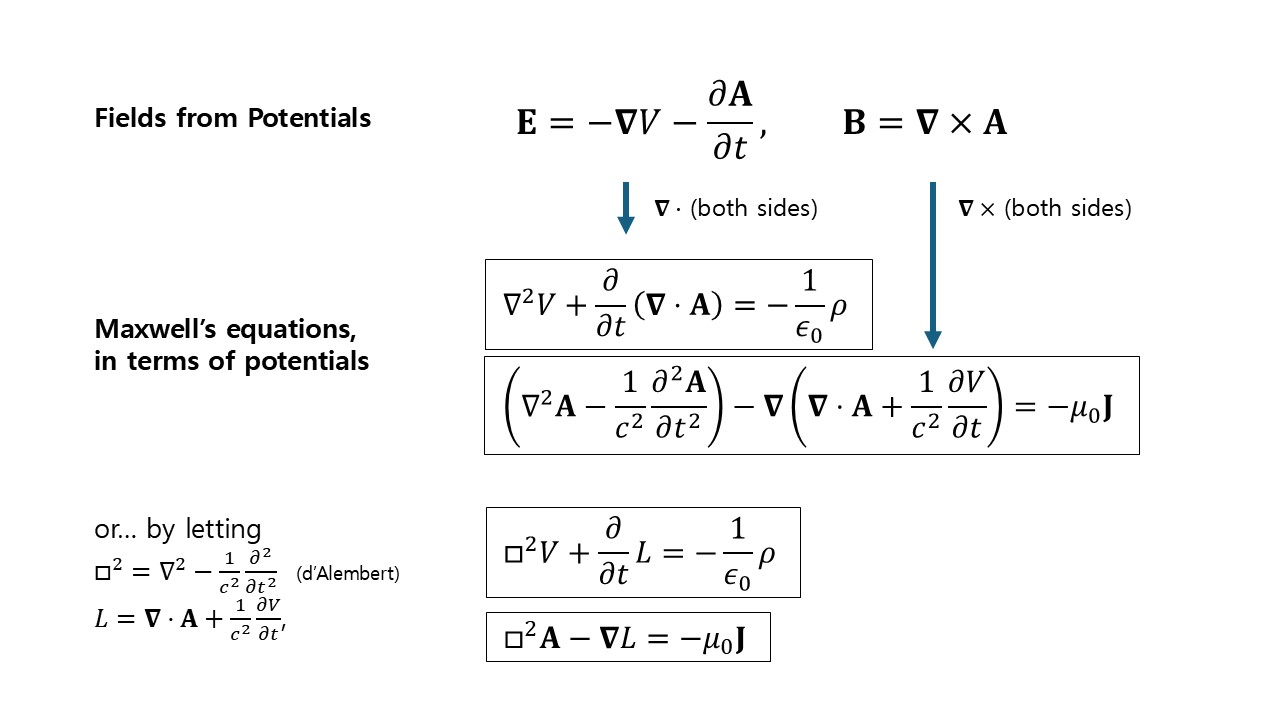
Maxwell's equations imply that there exist some 'potential' functions from which the field is obtained. The electric and magnetic field is related to the scalar and vector potential as follows.

Here, we observe that the entire Maxwell's equations can be reduced to two equations involving the potentials. (That is, the problem of solving for 6 components of two fields is reduced to solving for 4 components of the potentials!)

Gauge Transformations, Coulomb and Lorenz Gauge

From the relation between the potentials and the fields, we see that multiple different combination of potentials can result in the same fields. That is, we can impose additional conditions to potentials regarding our interest. Those are called gauge conditions. A gauge transformation alters the potentials but doesn't affect the fields (which are the observable, physical part).

We employ different gauge conditions in different situations. The Coulomb gauge, which we used in magnetostatics, assumes the vector potential is divergenceless, and results in the Poisson equation for the scalar potential.

In electrodynamics, the Lorenz gauge (not Lorentz) is a widely chosen setting. This condition results in inhomogeneous wave equations of the potentials, as shown above. The equation is often expressed with d'Alembertian, which is the Laplacian operator in Minkowski spacetime. The symmetry in the equations make the gauge useful in the context of special relativity.

Retarded Potentials, Jefimenko's Equations

Now, we know the general equations for the potentials, given the charge and current distributions. The inhomogeneous wave equations in Lorenz gauge looks much like the Poisson's equations, which we saw in electrostatics and magnetostatics. But now, we have time dependence in the charge and current densities.

We want to find the general potential expressions that satisfy the general equations. Can't we just integrate all over the space at time t, like what we did in static case? Things are more complicated then that; we have to consider that an electromagnetic 'news' travels at the speed of light. In other words, the 'timestamp' of a charge or current we see depends on the distance to the region. So, we should integrate those with retarded time.

The picture above shows the retarded potentials obtained by integrating all over the space with retarded time. But does these indeed satisfy the inhomogeneous wave equations? Yes, and the detailed proof is described in Griffith chapter 10.2.

We can bring back the relation between fields and potentials to obtain the general expression of fields. The expression shown above is called Jefimenko's equations.

Point Charge - Liénard-Wiechert Potentials

The field of a point charge was rather easy in static case. But it is a bit more complicated in dynamic case. The integral cannot be simply replaced with something like $q/r$, since in classical electrodynamics the point charge is not genuinely a point charge, but is thought as a continuous charge density concentrated in a very small volume. A geometric argument (illustrated below) states that an approaching volume seems larger, and a volume going away seems smaller to the observer. (note that this argument has nothing to do with special relativity.) This argument leads to Liénard-Wiechert potentials, the general potentials of a moving charge:

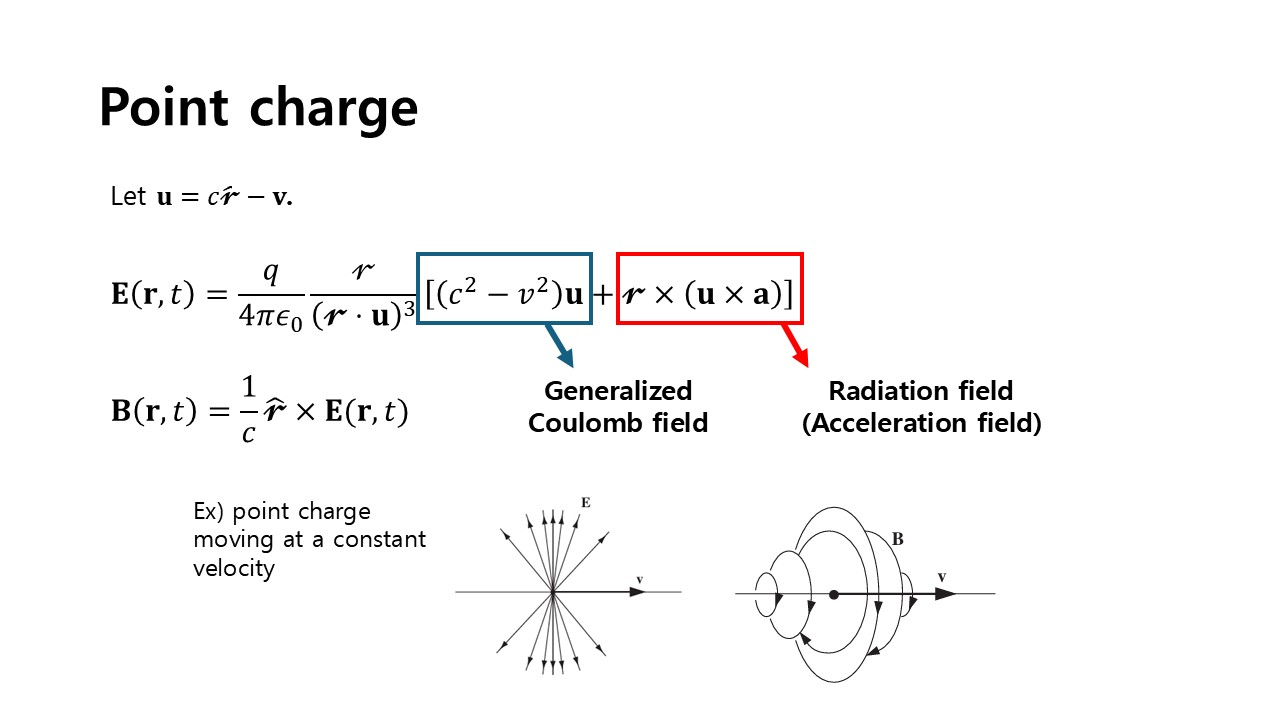
We can obtain the fields from these as well.

Here, we observe that the electric field contains the acceleration-dependent term. This term is called the radiation field or acceleration field, since it is involved with electromagnetic radiation of charges. The other term, which doesn't depend on the acceleration, is called the generalized Coulomb field or the velocity field.

References

1. David J. Griffith. <Introduction to Electrodynamics>. 5th ed. Chapters 10.1-10.3.