7.3. Maxwell's Equations

In mathmatics you don't understand things. You just get used to them.

- John von Neumann

We have seen several equations stating the relation between the electric and magnetic field. They are Maxwell's work; the equations were written in much more complicated forms back then. In this post, we will put together the Maxwell's four equations of electrodynamics.

The Displacement Current and Ampere's Law

The Ampere's law in magnetostatics,

$\nabla\times\mathbf{B}=\mu_0\mathbf{J}$

was derived from the integral form, which involves the current enclosed by Amperian loop.

$\displaystyle \oint\mathbf{B}\cdot d\mathbf{l}=\mu_0 I_{enc}$

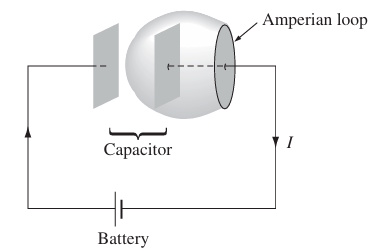
However, there can be many different 'enclosed surfaces' for an Amperian loop. This is not a serious problem in magnetostatics, as all currents are steady currents. So the $I_{enc}$ $\mu_0I_{enc}$is independent of the choice of enclosed surface. However, if current is different at different points, the $I_{enc}$ will be inconsistent. This leads to paradoxes like shown in the figure below:

When we set the Amperian loop like this, the 'enclosed current' becomes zero, even if the line integral of the magnetic field is nonzero. Therefore, we must also put into account something other than the current. Maxwell fixed the Ampere's law for electrodynamics, as follows:

$\displaystyle\nabla\times\mathbf{B}=\mu_0\mathbf{J}+\mu_0\epsilon_0{\partial\mathbf{E}\over\partial t}$

The extra term added is called the displacement current.

$\displaystyle\mathbf{J}_d=\epsilon_0{\partial\mathbf{E}\over\partial t}$

Adding this term makes the law mathematically seamless; It makes the divergence of both sizes zero. (Why? Recall the continuity equation and Gauss's law.)

Despite its name, displacement current is actually not a current (as no charge is involved). The modified Ampere's law implies that a changing electric field induces a magnetic field, even if there is no charge in motion.

Maxwell's Equations

Now, we have the Maxwell's four equations:

$\displaystyle \nabla\cdot\mathbf{E}={1\over\epsilon_0}\rho$ (Gauss's law)

$\displaystyle \nabla\cdot\mathbf{B}=0$ (No name)

$\displaystyle \nabla\times\mathbf{E}=-{\partial\mathbf{B}\over\partial t}$ (Faraday's law)

$\displaystyle\nabla\times\mathbf{B}=\mu_0\mathbf{J}+\mu_0\epsilon_0{\partial\mathbf{E}\over\partial t}$ (Ampere's law with displacement current)

together with the Lorentz force law,

$\mathbf{F}=q(\mathbf{E}+\mathbf{v}\times\mathbf{B})$

They summarize the entire classical electrodynamics theory. Maxwell's equations dictate how the charges and their motion produces fields, and the Lorentz force law dictates how fields affect charges.

In free space (i.e. when $\rho=0,\ \mathbf{J}=\mathbf{0}$ everywhere), Maxwell's equations become

$\displaystyle \nabla\cdot \mathbf{E}=0$

$\displaystyle \nabla\cdot \mathbf{B}=0$

$\displaystyle \nabla\times \mathbf{E}=-{\partial\mathbf{B}\over\partial t}$

$\displaystyle \nabla\times \mathbf{B}=\mu_0\epsilon_0{\partial\mathbf{E}\over\partial t}$

When the divergences of the fields are zero everywhere, we see a pleasing symmetry. A changing electric field induces a magnetic field. A changing magnetic field induces an electric field.

Maxwell's Equations in Matter

How can we write the Maxwell's equations more conveniently, in terms of the free charges and currents? We know that electric polarization and magnetization results in bound charge density and bound current density, respectively:

$\rho_b=-\nabla\cdot\mathbf{P}$ , $\mathbf{J}_b=\nabla\times\mathbf{M}$

Inside a medium, we write the charge density as a sum of free charge density and bound charge density.

$\rho=\rho_f+\rho_b$

Also, we wrote the current density as a sum of free current density and bound current density in magnetostatics. However, when polarization can change over time, the motion of bound charges also produces a current. It is called the polarization current.

$\displaystyle\mathbf{J}_p={\partial\mathbf{P}\over\partial t}$

So, in electrodynamics, the current density consists of three parts:

$\mathbf{J}=\mathbf{J}_f+\mathbf{J}_b+\mathbf{J}_p$

Let's explicitly write the charge density and current density, along with the definition of D-field and H-field:

$\rho=\rho_b-\nabla\cdot\mathbf{P}$

$\displaystyle\mathbf{J}=\mathbf{J}_f+\nabla\times\mathbf{M}+{\partial\mathbf{P}\over\partial t}$

$\mathbf{D}=\epsilon_0\mathbf{E}+\mathbf{P}$ $=\epsilon\mathbf{E}$

$\displaystyle\mathbf{H}={1\over\mu_0}\mathbf{B}-\mathbf{M}$ $\displaystyle={1\over\mu}\mathbf{B}$

Plugging in these identities in Maxwell's equations, we get the Maxwell's equation in matter (Note that this is not a 'more generalized' form, but the exact same equations merely written in a convenient form):

$\nabla\cdot\mathbf{D}=\rho_f$

$\nabla\cdot\mathbf{B}=0$

$\displaystyle\nabla\times\mathbf{E}=-{\partial\mathbf{B}\over\partial t}$

$\displaystyle\nabla\times\mathbf{H}=\mathbf{J}_f+{\partial\mathbf{D}\over\partial t}$

Boundary Conditions

Generally, the fields are discontinuous at a surface charge density, a surface current density, or the interface between two different media. They can be deduced the Maxwell's equations in integral form. (Recall the Gaussian pillboxes and Amperian loops.)

In summary, the explicit form of the discontinuities are

$D^{\perp}_{above}-D^{\perp}_{below}=\sigma_f$

$B^{\perp}_{above}-B^{\perp}_{above}=0$

$\mathbf{E}^{\parallel}_{above}-\mathbf{E}^{\parallel}_{below}=\mathbf{0}$

$\mathbf{H}^{\parallel}_{above}-\mathbf{H}^{\parallel}_{below}=\mathbf{K}_f\times\hat{\mathbf{n}}$

Maxwell's equations and their boundary conditions are the fundamental concepts in theories of electromagnetic waves, their reflection and refraction.

References

1. David J. Griffith. <Introduction to Electrodynamics>. 5th ed. Chapter 7.3.